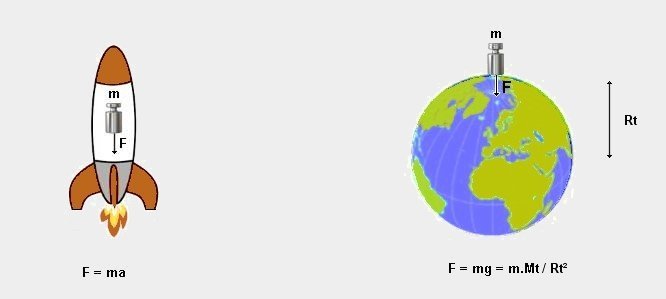
Principe d'équivalence

Hypothèse de départ :

Nous allons considérer qu'une même grandeur mesurable aura toujours les mêmes dimensions

Par exemple :

• Une longueur ou une distance aura toujours une dimension L ( et pourra se mesurer en mètres )
  
• Une surface aura une dimension L² ( et pourra se mesurer en m³ )
  
• Une vitesse sera évaluée par un espace par rapport à un temps L /T ( m / s )
  
• Une accélération pourra se mesurer en m / s² et aura comme dimensions L /T² ( m / s² )

Dans le cas d'une force, celle-ci peut provenir de :

• Force provenant de l'accélération d'une masse ( on écrit souvent F = ma )
  
• Force de gravitation (attraction des masses = loi de Newton )
  
• Force pour comprimer un ressort
  
• Force pour comprimer un gaz dans un cylindre
  
• Force subie par une charge dans un champ électrique etc.......

Conformément à notre hypothèse, de départ, toutes ces forces d'origines différentes devraient avoir les mêmes dimensions
En comparant la force pour accélérer une masse et la force d'attraction des masses ( loi de Newton ) que l'on pourra déduire les dimensions d'une masse en fonction de l'espace et du temps. Prétendre que ces deux forces ont les mêmes dimensions équivaut à affirmer que la constante de Newton n'a pas de dimensions ou bien que la masse dite " inerte " et la masse dite " gravifique " sont identiques donc cette constante de Newton ne serait que un nombre sans dimension K = 6,67 10 ^ -11

La loi d'attraction des masses de Newton :

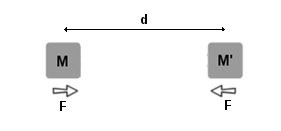
Nous savons par les lois élémentaires de physique que, en principe, deux masses M et M' séparées par une distance " R " sont attirées mutuellement par une force proportionnelle au produit des deux masses et inversement proportionnelle au carré de la distance qui les sépare suivant la formule bien connue

F = K (M.M')/d²

• F = la force qui attire M et M' l'une vers l'autre
• K = la constante de Newton
• M et M' = les deux masses considérées
• d = la distance qui sépare ces deux masses

Cela veut dire que chacune des deux masses est attirée vers l'autre avec une force F = K (M.M')/d²
donc M subit une accélération égale à F / M = K M'/d²
Aussi M' subit une accélération égale à F / M' = K M /d²

Um cas particulier .... la masse M = m = 1 Kg et la masse M' = Mt = masse de la Terre

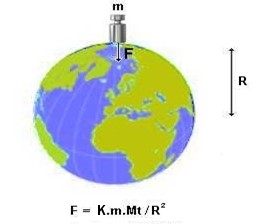
Dans ce cas ci, la force F agissant sur m ( et aussi sur Mt ) est égale à K.m.Mt / R² ( m.g = 9.81 Newtons )
L'accélération de m sera donc égale à F / m = K.Mt / R² ( accélération de la pesanteur = 9.81 m/s² = g )
L'accélération subie par la terre sera, elle, négligeable ( F / Mt = K.m / R² sera de l'ordre de 10 ^ (-24) m /s²

Le principe d'équivalence :

Les effets d'un champ gravitationnel sont identiques aux effets d'une accélération du référentiel de l'observateur,
Dans les deux expériences ci dessous il sera en principe, impossible de distinguer si elles ont été réalisées sur la terre dans un laboratoire fixe et immobile, ou bien à l'intérieur d'une fusée qui accélère dans l'espace de façon continue à 9.81 m/s²

,
Une masse unitaire m soumise dans l'espace à une accélération de 9.81 m/sec (dans une fusée par exemple) subit la même force F que celle que subit cette même masse m soumise à l'attraction terrestre..
Ces deux forces sont de même nature ( identiques, rien ne pourrait les distinguer), elles devraient donc avoir les mêmes dimensions.

D'un côté elle s'exprime comme F = ma et a comme dimensions M L / T ²        (1)

De l'autre côté on a F = K.m.Mt / Rt² et a comme dimensions M² / L²              (2)


Avec

• Mt la masse de la terre ( de dimension M )
• Rt le rayon de la terre ( de dimension L )

En comparant les dimensions de (1) avec (2) on a   M L / T ² = M² / L²     soit   M = L³ / T ²

Donc les dimensions d'une masse seraient : M = L³ / T ²

Dans (2) la constante de Newton K est ici considérée comme un simple nombre sans dimensions 6,67 10 ^ (-11)

Quel est l'intérêt de considérer la masse comme un volume par un temps au carré ( L³ / T ² ) ?

Pouvoir grouper dans un même tableau beaucoup de grandeurs physiques, mécaniques et électriques, ainsi que leurs interdépendances ( diagrammes espace-temps )  Permet d'établir une relation étroite entre la mécanique classique et l'électromagnétisme, la charge devient simplement une masse " complexe " ( voir plus loin, " dimension de la charge électrique " )