1. Grandeurs fondamentales :

On considère une grandeur mesurable comme fondamentale quand celle-ci ne dépend pas d'une autre grandeur, par exemple on considère généralement le temps ( T ) et l'espace ( L ) comme grandeurs fondamentales

2. Grandeurs non fondamentales :

La plupart des grandeurs mesurables en physique ne sont pas fondamentales et dépendent directement d'autres grandeurs dites fondamentales comme le temps T et l'espace L, … Voici quelques exemples ;

• Une surface dépend directement du carré des longueurs les dimensions d'une surface sont L²
  
  
• Un volume va dépendre de la troisième puissance de l'espace et aura comme dimensions L³
  
  
• Une vitesse d'un point A par rapport à un point B est en fait la variation par rapport au temps de la distance ( un espace ) qui sépare le point A du point B : un rapport entre un espace et un temps, ce sera par exemple des mètres par seconde. Les dimensions d'une vitesse seront L / T
  
  
• Une accélération ( variation d'une vitesse par rapport au temps ) se mesure en mètres par secondes par seconde soit en m / s², soit un espace par rapport à un temps au carré, les dimensions d'une accélération seront de L / T²

Imaginons maintenant qu'il soit possible d'isoler une partie de l'univers dans un espace fermé, un genre de grand aquarium (sans eau) par exemple, Dans cet espace isolé du reste on peut imaginer les situations suivantes :

Que se passerait-il si tout l'espace ( les distances L ) se rétrécissait de moitié ?

Um monde où brusquement toutes les longueurs seraient réduites de moitié

• Les mesures de surfaces seraient réduites au quart de leur valeur initiale *
  
• Les mesures de volumes seraient réduites au huitième de leur valeur initiale *
  
• Les mesures de vitesses seraient réduites de moitié
  
• Les mesures d'accélérations seraient aussi réduites de moitié

* Dans le cas de la surface d'un disque ou du volume d'une sphère par exemple on considère que la valeur de   pi   reste constante ( 3,14... )

On voit donc que, dans le cas d'un rétrécissement, de l'espace L certaines mesures seraient affectées, ce sont les mesures de grandeurs qui dépendent de l'espace L et donc qui contiennent L dans leurs dimensions

Si la mesure d'une grandeur varie conformément à une variation de l'espace L on pourra dire que cette grandeur contient l'espace L dans ses dimensions.

Que se passerait-il si le temps T diminuait de moitié ? ( tout irait plus vite . . . )

• Les mesures de longueurs seraient inchangées
  
• Les mesures de surfaces seraient inchangées
  
• Les mesures de volumes seraient inchangées
  
• Les mesures de vitesses seraient le double de leur valeur initiale
  
• Les mesures d'accélérations seraient le quadruple de leur valeur initiale

Ici aussi on voit que, dans le cas d'un diminution du temps T, ( une heure deviendrait ½ heure par exemple, donc pour parcourir une même distance on mettrait la moitié du temps ) les mesures affectées seraient les mesure de grandeurs qui dépendent du temps T c'est-à-dire qui contiennent T dans leurs dimensions.

Dans les deux cas on peut constater que si une grandeur contient l'espace L et /ou le temps T dans ses dimensions, la mesure de cette grandeur varie conformément aux variations subies par l'espace et / ou le temps
L'inverse est vrai aussi : si une grandeur varie suivant les variations subies par l'espace et/ou le temps, on pourra en conclure que l'espace et / ou le temps, interviennent dans les dimensions de cette grandeur

3. Constantes de proportionnalité sans dimensions :

On peut comparer deux grandeurs de mêmes dimensions à l'aide de d'une constante de proportionnalité, c'est généralement le cas pour exprimer une unité par rapport à une autre, par exemple

• Un pouce = 25.4 mm ( 2 mesures dans l'espace L )
  
• Une heure = 3600 secondes ( 2 mesures du temps )
  
• Un hectare = 10.000 m² ( 2 surfaces )
  
• Un baril de pétrole = 159 litres ( 2 volumes )
  
• Un km / heure = 27,7 cm /s ( 2 vitesses )

Ces constantes de proportionnalités sont des nombres sans dimensions

4. Constantes de proportionnalité avec dimensions :

Dans la vie courante, souvent on mélange les dimensions sans s'en rendre compte.

Pour répondre à une question " Es-tu encore loin ?" On répondra par exemple " une demie heure de route "
" Une demie heure de route " pour vouloir dire " 40 Km "

En fait ici on compare un temps ( 1/2 heure ) à un espace ( 40 km ) ce qui n'a pas de sens, mieux serait de dire :
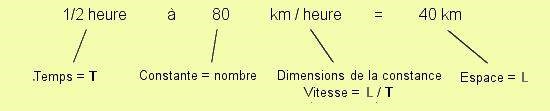
" une demie heure à 80 km/h " = " 40 Km "

Dans cette égalité nous avons 3 parties :

1. " une demie heure = ( 1/2 x temps ( 1 / 2 T )
2. " 80 km/h = 80 x espace / temps ( 80 L / T )
3. " 40 Km = 40 x espace ( 40 L )

Une demie heure à 80 km/h = 40 Km devient :

1 / 2 x T x 80 x L / T = 40 x L
1 / 2 x 80 x ( T x L / T ) = 40 x L
1 / 2 x 80 L = 40 L ( on a simplifié par " T " )
1 / 2 x 80 km = 40 km ( km = unité d'espace )

Pour finir nous avons bien un espace égal à un espace ce qui a un sens.
Pour égaler un temps ( 1/2 heure ) à un espace ( 40 km ) il faut rajouter le terme :

"en voiture qui roule à 80 km/h" ou tout simplement " à 80 km/h"
Que nous allons appeler " constante de la voiture " qui sera 80 km/h dans cet exemple.
Cette constante a une dimension ( une vitesse = km/h ) ce ne sera pas simplement " 80 " mais ce sera 80 km/h
( si on change d'unités la valeur numérique de la constante de la voiture change aussi: 80 km/h = 22.2 m/s )

La même constante pour un avion serait par exemple 800 km/h et pour une bicyclette 35 km/h
Pour égaler un temps à une longueur ( espace ) il faut rajouter une constante qui aura les dimensions d'une vitesse.

Autres exemples de constante de proportionnalité avec dimensions :

Si on demande à quelqu'un " combien as-tu vendu de kilos de café " et que l'on répond " 200 sacs "
la réponse correcte serait " 200 sacs à 60 kg/sac = 12,000 kg " La constance qui relie les sacs de café avec des kilos de café est de 60 kg/sac et aura comme dimension des kg/sac Ici encore on ne peut pas construire une égalité avec des " sacs de café " d'une part et des " kilos de café " d'autre part il faut savoir combien de kilos il y a dans chaque sac de café pour compléter l'égalité..
La constante de proportionnalité sera ici 60 avec comme dimension Kg/sac

Avec deux pleins d'essence je fais 800 km quelle est la consommation en litres pour ces 800 Km ? Il faut savoir combien de litres d'essence représente un plein, l'équation correcte serait :
2 pleins d'essence à 35 litres par plein = 70 litres
Ici la constante sera 35 " litres par plein " ( dimension de la constante = litres par plein )