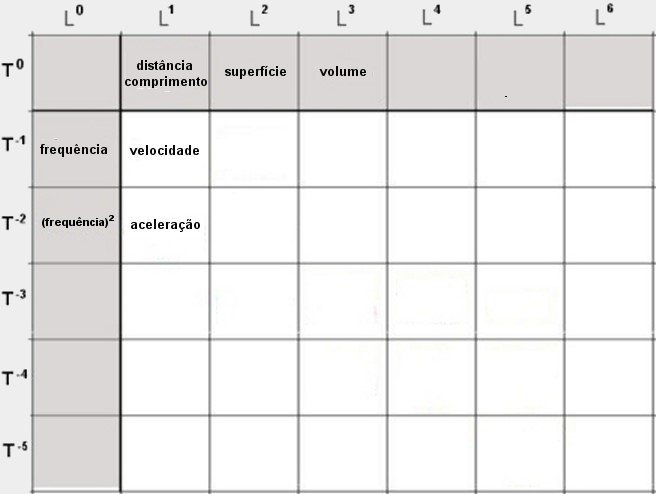
Aqui podemos visualizar, na forma de um quadro, as dimensões de algumas grandezas em física.
Na linha superior vamos encontrar as diferentes Na linha superior temos as diferentes atribuições de L , ou seja, Lo, L1 , L2 , L3 , L4, L5, L6
Na coluna da esquerda as atribuições negativas de T , ou seja T0, T -1 , T -2 , T -3 , T -4 , T -5

• Um comprimento ou distância ( dimensão L ) encontra-se na casa L1T0
• Uma superfície ( dimensão L² ) encontra-se naturalmente na casa L2 T0
• Um volume ( dimensão L³ ) encontra-se naturalmente na casa L3 T0
• Uma velocidade ( dimensão L / T ) encontra-se na casa L1 T - 1
• Uma aceleração (dimensão L / T ² ) encontra-se na casa L1 T - 2
• Uma frequência (dimensão 1 / T ) encontra-se na casa L0 T - 1
  

Também teremos:

• O quadrado da frequência ( dimensão 1 / T ² ) na casa L0 T - 2
• O fluxo = volume por segundo ( dimensão L³ / T ) na casa L³ T - 1
  

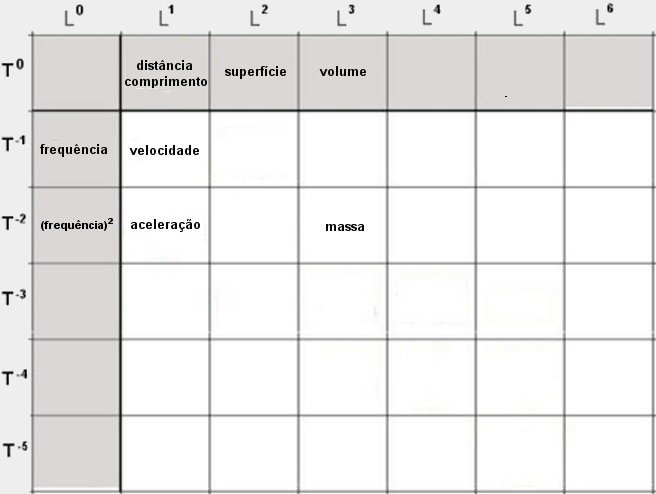
A massa = L³ / T²

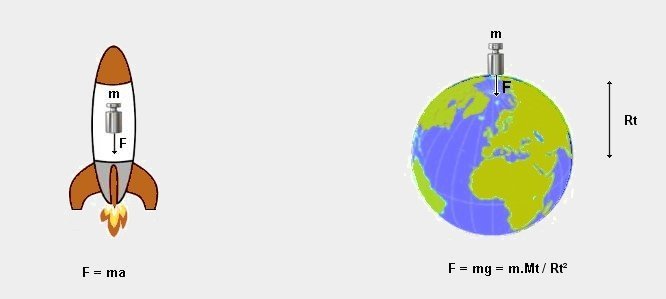
, Uma massa unitária m submetida, no espaço, a uma aceleração de 9,81 m/s (dentro de um foguete, por exemplo) sofre a mesma força F que esta mesma massa m quando submetida à atração terrestre.

Estas duas forças são de mesma natureza (em princípio idênticas, nada poderá distingui-las). Assim, elas deverão ter as mesmas dimensões. Aqui vamos considerar, portanto, que a massa dita "inercial" e a massa dita "gravitacional" são exatamente a mesma coisa.

De um lado ela se expressa como F = ma   e tem como dimensões  M . L / T²       (1)
De outro lado temos F = K.m.Mt / Rt²   e tem como dimensões   M² / L²             (2)

Com Mt a massa da terra (de dimensão M) e Rt o raio da terra (de dimensão L)
Comparando as dimensões de (1) com (2) temos M . L / T² = M² / L²

Assim as dimensões de uma massa serão M = L³ / T²     ( vide apêndice 1 )
Poderemos a partir daqui exprimir a massa em kg ou em m³ / s²   ( vide apêndice 2 )

Em (2) a constante de Newton K é aqui considerada como uma simples número sem dimensões.

Algumas outras grandezas ;

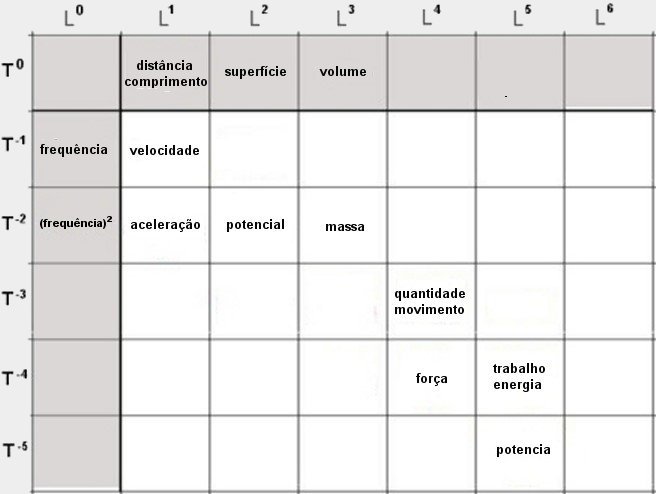
Grandezas importantes en fisica :

• A quantidade de movimento ou impulso ( massa . velocidade ) encontra-se na casa L4 T -3
• A força ( massa . aceleração ) encontra-se na casa L4 T -4
• O trabalho ou energia ( força . deslocamento) encontra-se na casa L5 T -4
• A potência ( energia / tempo ) encontra-se na casa L5 T -5
• O potencial ( energia / massa ) ou ( massa / distancia ) encontra-se na casa L2 T -2

Também teremos:

• A pressão ( força / superfície ) na casa L2 T -4
• A rigidez de uma mola ( força / deslocamento ) na casa L³ T -4
• O quadrado da massa ( massa . massa ) na casa L6 T -4
• O quadrado da velocidade ( velocidade . velocidade ) na casa L2 T -2
• O quadrado da frequência ( frequência . frequência) na casa T -2
• A ação ( energia . tempo) na casa L5 T -3

Densidade

A densidade D pode ser definida como massa / volume : L3 T -2 / L3 = D = T -2 supondo D x T 2 = constante
Supondo a " densidade . T ² = N = constante " o que poderia explicar que num sistema onde a densidade de massa é muito fraca teremos uma tendência a ter fenômenos com períodos muito grandes e vice versa.
Uma galáxia, por exemplo ( densidade média de massa excessivamente fraca ) terá um período de rotação muito grande, da mesma forma que dentro de um núcleo atômico ou numa região super densa ( densidade de massa muito grande ) ocorrerão fenômenos periódicos muito rápidos ( frequências muito elevadas).
Se consideramos como densidade D a densidade média de uma esfera de raio Terra-Sol, contendo a massa do Sol, e o valor de N = 3 p / K = 1,413 10^11 ( K = constante de Newton )   T²  terá como valor o quadrado do período de revolução da Terra em torno do Sol , ou seja  T² = 9,97 10 ^14 segundos ( T = 31,575,000 secundos = 365,25 dias).

Caso da Terra em órbita em torno do Sol, teremos:

Densidade . T ² = N = 3 p / K
T ² = ( 3 p / K ) / D   

• D = massa da Terra / { 4/3 p ( Raio Terra -Sol)³ } = 1,4115 10 ^-4 kg / m³
• 1 / D = ( 7,068 10 ^3 ) m³ / kg
• T ² = N / D = ( 1,413 10 ^11 ) . ( 7,068 10 ^3 ) = 9,97 10 ^14
• T = ( 9,97 10^14 ) ^1/2 = 31,59 10 ^6 sec = 365,25 dias ( T = período de revolução em torno do sol)

Algumas relações fundamentais em física

M.a = F          ( L3 T -2 )( L1 T -2 )   =   ( L4 T -4 )     =>     massa . aceleração = força
M.v = p          ( L3 T -2 )( L1 T -1 )   =   ( L4 T -3 )     =>      massa . velocidade = impulsão ( momentum )
M.v² = E        ( L3 T -2 )( L2 T -2 )   =   ( L5 T -4 )     =>     massa . (velocidade)² = energia
M/R² = a       ( L3 T -2 )( L-2 )   =   ( L1 T -2 )            =>     massa / (distância )² = aceleração ( g = Mt / R² )
M²/R = E      ( L3 T -2 )² (L-1)  =  ( L5 T -4 )              =>     (massa)² / (distância ) = energia
M²/R² = F    ( L3 T -2 )² (L-2)  =  ( L4 T -4 )              =>     (massa)² / (distância )² = força
F.L = E           ( L4 T -4 )( L )  =  ( L5 T -4 )                   =>     Force . distância = energia ( trabalho )
F / L = k        ( L4 T -4 )( L-1 )  =  ( L3 T -4 )                =>     Force / distância = rigidês (de uma mola por exemplo)
k / M = T -2  ( L3 T -4 )( L-3 T 2 ) = ( L0 T -2 )          =>     rigidês / massa = quadrado da frequência
F . v = W        ( L4 T -4 )( L1 T -1 )  =  ( L5 T -5 )         =>     força . velocidade = potência
p / T = F        ( L4 T -3 )( L0 T -1 )  =  ( L4 T -4 )         =>     impulsão / tempo = força