|
masse dimension mass dimension dimension mass dimension
mass dimensiass dimension dimension mass dimension mass dimensionsion
En écrivant les formules de l'attraction de deux masses M ( Loi
de Newton ) et de deux charges Q ( Force de Coulomb ) ce sont deux forces
de signes opposés ( attraction et répulsion ) Cette force
vaut à une constante près :
QQ/R² =
( -1 ) MM/R²
(1)
QQ =
( i ² ) MM
(2)
Nous avons de chaque côté de (1)
une " Force " qui devraient avoir les mêmes " dimensions
"
Cette force sera dite " négative" dans le cas d'attraction
( deux masses qui s'attirent suivant Newton ) et " positive",
( cas de deux charges électriques de même signe qui se repoussent
suivant la formule de Coulomb )
L'équation (2) donne deux solutions
pour Q ==>> Q = i M et Q = - i M avec i² = - 1
Nous aurons ainsi deux types de charges électriques avec comme
dimensions : i M et - i M , ou encore i L³/T² et - i L³/T²
Ces deux types de charges seront appelées " charge positive
" et " charge négative "
On verra immédiatement que deux charges de même signes se
repoussent ( force positive ) et deux charges de signes contraire auront
tendance à se rapprocher ( force négative ) De même
deux masses positives ou négatives ( s' il en existe ) auront tendance
à se rapprocher (force négative) tandis que deux masses
de signes contraires auront tendance à s'écarter l'une de
l'autre ( force positive ) suivant la même formules de Newton (
en 1/ R² )
Les dimensions de la charge seront donc les mêmes que les dimensions
de la masse, mais complexes i L³/T² ou
- i L³/T² certaines grandeurs électriques
auront des dimensions " complexes " i est
un nombre dit " complexe " défini par la relation : i
² = - 1
On pourrait même
supposer que une déformation " espace - temps " aurait
une partie réelle ( masse ) et une partie complexe (charge) d'une
façon générale M + iQ et la formule générale
d'attraction des" masses - charges" devient :
F = ((M1+iQ1).(M2+iQ2))/R²
(3)
Cette force aura
deux composantes réelles ( deux masses s'attirent et deux charges
de même signes se repoussent )
((M1).(M2))/R²
et ((iQ1).(iQ2))/R²
Cette même force aura deux composantes complexes ( une charge n'ayant
pas d'effet sur une masse )
((M1).(iQ2))/R² et ((M2).(iQ1))/R²
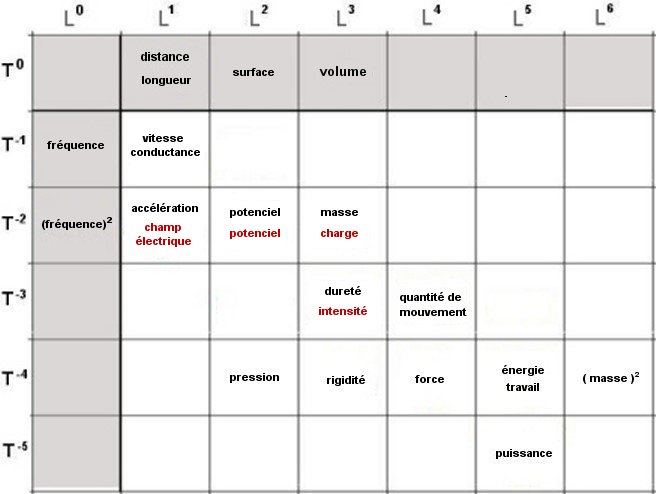
Grandeurs complexes
en rouge
Sachant que la charge électrique a comme dimensions i L3 T -2 nous
pouvons déterminer les dimensions de :
- L'intensité
I ( Ampères ) = Coulombs / seconde soit i L3 T -2
/ T = i L3 T -3
- Le potentiel V
( Volts ) = Coulombs / mètres soit i L3 T -2 / L
= i L2 T -2
- Le champs électrique
= Volts / mètres soit i L2 T -2 / L = . i L T -2
Ces mêmes grandeurs peuvent varier par rapport au temps :
- l'intensité
par rapport au temps soit i L3 T -3 / T = i L3 T -4
- Variation de potentiel
par rapport au temps soit i L2 T -2 / T = i L2 T -3
- Variation du champs
électrique par rapport au temps soit i L T -2 / T =
i L T -3
Les grandeurs électriques
( charge, potentiel, intensité, champ électrique…)
deviendraient donc des grandeurs complexes contrairement aux grandeurs
mécaniques qui seraient réelles et donc directement mesurables
Pour mesurer une grandeur électrique ( charge, potentiel, intensité,
champ électrique,… ) il faut nécessairement utiliser
l'électricité pour obtenir une grandeur réelle mesurable
( force ou déplacement par exemple )
Une charge donnera une force ( mesurable directement ) avec une autre
charge ou bien avec un champs électrique par exemple, en combinant
deux grandeurs complexes ( i²) on retombe sur du réel mesurable.
Par exemple une charge (grandeur complexe ) située dans un champ
électrique ( autre grandeur complexe ) donnera donc une force (
grandeur réelle ) qui aura les mêmes dimensions qu'une force
mécanique ( L4 T -4 ) . Aussi on peut voir qu'un potentiel électrique
(V) avec une intensité ( ampères A ) donnera une puissance
( W = VA ) qui aura les mêmes dimensions qu'une puissance mécanique
( L5 T -5 )
Par contre une charge (grandeur complexe ) située dans un champ
gravifique (grandeur réelle) donnera une grandeur non mesurable
( force complexe ? )
Quelques
relations en électromécanique ( Les grandeurs
complexes sont en rouge on écrira "
L3 T -2 " pour "
i L3 T-2" )…
Q.Ê = F
( L3 T -2 ) ( L1 T -2 )
= (
L4 T -4 ) => Charge
. Champ électrique = Force
Q.V = E (
L3 T -2 ) ( L² T -2 )
= ( L5 T -4 ) => Charge
. Potentiel = Energie
Q / R = V
(
L3 T -2 ) ( L -1) = ( L2
T -2 ) =>
Charge / distance = Potentiel
Q / R² = Ê
( L3 T -2 ) ( L-2 ) = (
L1 T -2 ) =>
Charge / (distance)² = .
Champ électrique
Q² / R = E (
L3 T -2 )²
/ (L-1) = ( L5 T -4 ) =>
(Charge)² / distance = (Charge)²
/ capacité = Energie
Q² / R² = F (
L3 T -2 )² / ( L-2 ) = ( L4 T
-4 ) => (Charge)²
/ (distance)² = Force
V.I = W
( L2 T -2 ) ( L3 T -3 ) =
( L5 T -5 ) => Potentiel
. Intensité = Puissance
I / V = 1 / R (
L3 T -3 ) ( L-2 T 2 ) = ( L1 T -1 ) =>
Intensité / Potentiel
= Conductance = 1/ Résistance
V.V = F (
L2 T -2 ) ( L2 T- 2 ) = ( L4 T -4 ) =>
Potentiel . Potentiel
= Force
( Î /T ) S = V (
L3 T-4 ) ( L-1 T 2 ) = ( L2 T -2 )
=> (Variation d'intensité).(
Coef self-induct ) = Potentiel
C V = Q
( L1 T 0 )( L2 T -2 )
= ( L3 T -2 ) =>
Capacité . Potentiel = Charge
I² . R
= W ( L3 T -3 )²
(L-1 T 1) = ( L5 T -5 ) => (Intensité)²
. (résistance ) = Puissance
Dimensions
de quelques grandeurs en physique
action = ( L5 T-3
) = énergie . temps
accélération = ( L1 T -2 )
capacité = ( L1 T 0 ) = longueur ou distance
champ électrique
( L1 T -2 ) ( Volts / mètre )
champs gravifique ( L1 T -2 )
charge ( L3 T -2 )
( Coulomb )
conductance ( L1 T -1 ) = 1 / résistance ( vitesse )
dureté ( L3 T -3 )
énergie ( L5 T -4 ) = travail ( Joule )
force ( L4 T -4 ) ( Newton )
inductance ( L-1 T 2 ) = 1 / accélération (
Henry )
intensité ( L3 T -3 ) ( Ampère
)
impulsion ( L4 T -3 ) ( momemt )
masse ( L3 T -2 )
potentiel électrique ( L2 T -2 ) (
Volt )
potentiel gravifique ( L2 T -2 )
pression ( L2 T -4 ) ( Bar )
puissance ( L5 T -5 ) ( Watts )
résistance ( L-1 T 1 ) = 1 / vitesse
rigidité ( L3 T -4 )
vitesse ( L1 T -1 )
|
![]()
![]()