Energie d'une quantité de mouvement :
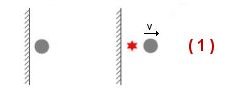
Figure (1)
Pour
mettre une masse en mouvement avec une vitesse v, supposons que soit
nécessaire une certaine quantité d’énergie représentée
ici par une étoile rouge.
( ce serait par exemple l´'énergie contenue dans un ressort)
Pour ce faire il faut biens sûr prendre appui sur une base fixe, par
exemple un mur de pierre.
On considère que l'appui (ce mur de pierre par exemple) a une masse infinie.
L’énergie nécessaire sera évidemment proportionnelle
à la masse, si l’on met en mouvement
deux masses égales il faudra, bien sûr, le double d’énergie
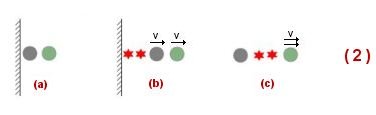
Figure (2)
Pour
mettre la même masse en mouvement avec une vitesse double 2.v,
l’expérience montre qu’il sera nécessaire 4 fois
plus d’énergie en effet :.
- Supposons deux masses égales au repos, une grise et une verte (a)
- Avec deux énergies unitaires, elles parviennent chacune à une vitesse v (b)
- Ensuite,
de nouveau avec deux énergies unitaires la masse grise revient
au repos
et la verte prend une vitesse double 2.v (c)
On
remarquera que pour doubler la vitesse de la masse verte, passer de (b)
en (c)
il fallait un appui ( il n’y avait plus le mur pour s’appuyer
! ) et donc on avait besoins de
renvoyer une masse égale ( grise ) avec la même vitesse opposée.
La masse grise (qui est revenue au repos) a été nécessaire
dans cette opération
et a consommé deux quantités d’énergie.
Donc
pour donner à une masse une vitesse double il a fallu 4 fois plus d’énergie
que
dans le cas précèdent..
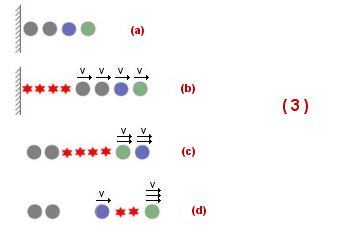
Figure (3)
Pour
mettre la même masse en mouvement avec une vitesse triple 3.v,
l’expérience montre qu’il sera nécessaire 9 fois
plus d’énergie en effet :.
- Supposons quatre masses égales au repos, deux grises et une bleue et une verte (a)
- Avec quatre énergies unitaires, elles arrivent chacune à une vitesse v (b)
- Ensuite,
avec quatre énergies unitaires les masses grises reviennent au
repos
et les masses verte et bleue arrivent à une vitesse double 2.v (c) - Et
pour finir avec deux énergies unitaires, la masse verte prend une
vitesse triple
et la masse bleue revient à une vitesse unitaire (d)
On remarquera que pour tripler la vitesse on a utilisé dix énergies
unitaires, une a été
nécessaire pour donner à la masse bleue une vitesse v et neuf
autres pour donner à la
masse verte une vitesse de 3v
On
peut montrer que pour obtenir une vitesse 4 fois plus grande il faudra dépenser
16
énergies unitaires et ainsi de suite
Conclusion : pour mette une masse en mouvement il faudra une énergie
•
Proportionnelle á la masse
• Proportionnelle au carré de la vitesse
Energie d'une quantité de mouvement :
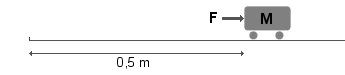
Soit
une masse unitaire M ( 1 kg ) que l'on pousse avec une force
F de 1 Newton pendant 1 seconde.
Par définition du Newton la masse M va acquérir
une vitesse de 1m/sec
La quantité de mouvement totale de M sera de 1 kg.m/sec
= 1 Pu
- la vitesse initiale = 0 m/sec
- la vitesse finale = 1 m/sec
- la vitesse moyenne = 0,5 m/sec
- la distance parcourue = 0,5 m/sec x 1 sec = 0,5 m
- énergie reçue par kg = 1 Newton x 0,5 m = 0,5 Joule
- énergie totale reçue = 0,5 Joule
Rappelons
que par définition 1 Newton appliqué sur une masse de 1 kg pendant
1 seconde
accélère cette masse de 1 kg / sec² ( augmente
la vitesse de cette masse de 1m/sec )
Maintenant
on applique encore 1 Newton pendant 1 seconde, Par définition du Newton
la masse
M va accélérer donc acquérir une vitesse
de 1m/sec en plus = 2 m/sec :
La quantité de mouvement totale de M sera de 2 kg.m/sec
= 2 Pus
- la vitesse initiale = 1 m/sec
- la vitesse finale = 2 m/sec
- la vitesse moyenne = 1,5 m/sec
- la distance parcourue = 1,5 m/sec x 1 sec = 1,5 m
- énergie reçue par kg = 1 Newton x 1,5 m = 1,5 Joule
- énergie totale reçue = 0,5 + 1,5 = 2 Joules
On peut continuer ainsi le raisonnement, pour arriver à une quantité de mouvement de
- 3 Pus ( 3 kg.m/sec ) l'énergie totale reçue = 0,5 + 1,5 + 2,5 = 4,5 Joules = (3²) / 2 Joules
- 4 Pus ( 4 kg.m/sec ) l'énergie totale reçue = 0,5 + 1,5 + 2,5 + 3,5 = 8 Joules = (4²) / 2 Joules
- 5 Pus ( 5 kg.m/sec ) l'énergie totale reçue = 0,5 + 1,5 + 2,5 + 3,5 + 4.5 = 12,5 Joules = (5²) / 2 Joules
On
voit donc que, avec une masse unitaire, pour arriver à une vitesse
v il faudra transmettre une
énergie de E = M.v²/2. ( soit
E = v²/2 avec M = 1 )
xxxxxxxxxxxxxxxxx