Énergie et capacité électrique  

 

Capacité d'une charge électrique :             

Voici une façon de voir comment la capacité représente donc la distance moyenne
entre les charges élémentaires :

              

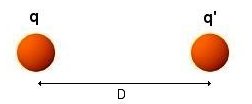
Considérons deux charges unitaires positives q et q' séparées par une distance D

La force qui tend à les séparer sera de : F = - k ( q.q' ) / D²   soit encore F = -k / D²
L'énergie de ce système sera donc de E = k ( q.q' ) / D  soit encore E = k / D
Avec k = 1/(4πεo) = c²/10,000,000

Cette énergie E represente le travail qu'il a fallu pour rapprocher les deux charges q et q'
de l'infini jusqu'à la distance D

                                              

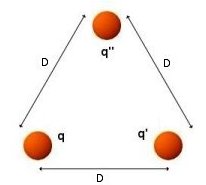
Dans le cas de trois charges unitaires positives q , q' et q" séparées entre elles par une distance D
Il faudra rapprocher une troisième charge q" des deux premières q et q' qui forment déjà une charge
double de 2q.

La force qui tend à les séparer sera de : F = - k ( 2q.q" ) / D²   soit encore F = - 2k / D²
L'énergie pour rapprocher q" de q et q' sera donc de E = k ( 2q.q" ) / D  soit encore E = 2k / D

L'énergie de ce système sera E = k / D  ( travail nécessaire pour rapprocher les charges q et q' )
et il faudra y rajouter E = 2k / D   ( travail nécessaire pour rapprocher la troisième charge q" de q et q' )
Le travail total ( énergie du système ) sera donc de ( k/ D ) + ( 2k / D )

                      

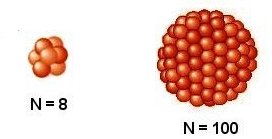
Dans le cas de 8 charges uniaires positives séparées entre elles par une distance moyenne D :
Le travail total pour les rapprocher les unes des autres ( énergie du système ) sera donc de :
E = (k/D) + 2(k/D) + 3(k/D) + . . . + 7(k/D) = 28(k/D)

Et pour 100 charges unitaires positives séparées entre elles par une distance moyenne D :
E = (k/D) + 2(k/D) + 3(k/D) + . . . + 98(k/D) + 99(k/D) = 4950(k/D) = 5000(k/D) - 50(k/D) = [(1/2)(100)² - 100/2].(k/D)

Et pour n charges unitaires positives séparées entre elles par une distance moyenne D :

E = [(1/2)(n)² - n/2].(k/D) = (1/2)(k/D)(n)² - (1/2)(k/D)(n)           (1)

À cela il faut rajouter l'énergie propre de chacune des charges unitaires :
E = (1/2)CV² = (1/2) q²/C  = 1/2C   pour chacune ( avec q =1 = CV ) C étant la capacité
de chacune de ces charges, ce qui donne pour n charges unitaires un total de

E = n/2C = (1/2)(1/C)(n)       (2)

E ( total ) = (1/2)(k/D)(n)² - (1/2)(k/D)(n) + (1/2)(1/C)(n)          (3) = (1) + (2)

L'énergie d'une charge q composée de n charges unitaires ( q = n ) vaut aussi q²/2C = n²/2C = (1/2)(1/C)(n)²

E ( total )   =   (1/2)(k/D)(n)² - (1/2)(k/D)(n) + (1/2)(1/C)(n) = (1/2)(1/C)(n)²

Donc :

(k/D)(n)² - (k/D)(n) + (1/C)(n) = (1/C)(n)² ==> (k/D)(n) - (k/D) + (1/C) = (1/C)(n)

(k/D)(n) - (k/D) + (1/C) = (1/C)(n) ==> [(k/D)- (1/C)] (n) = (k/D)- (1/C)

Et on trouve que (k/D) = (1/C)     ou bien     C = D/k    ou encore     D = C.k 

La capacité représente donc la distance moyenne entre les charges élémentaires.

 

 

Modifier la capacité d'un condensateur :

    

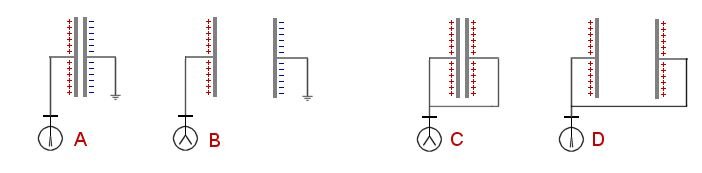
Considérons les cas de 4 condensateurs A, B, C, D, chacun munis d'un électroscope ( Voltmètre ).

Pour passer de A à B on a dû écarter les plaques d'un condensateur et fournir une énergie
pour séparer des charges opposées. La configuration B aura donc une énergie interne supérieure
pour la même charge, donc un potentiel plus élevé et une capacité moindre ( V plus grand )

Pour passer de C à D , en séparant les plaques, le condensateur a fourni une énergie en écartant
des charges de même signe . La configuration D aura donc une énergie interne inférieure
pour la même charge, donc un potentiel moins élevé et une capacité plus grande.
( en effet en D la distance moyenne entre les charges de même signe est plus grande )

                  

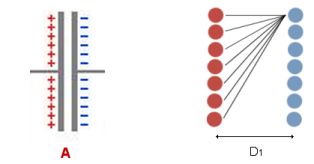
Le condensateur A pourra être comparé à deux ensembles de charges, un ensemble de charges
positives et un ensemble de charges négatives. Ces deux ensembles sont séparés par une
distance moyenne D1.
Chacun de ces ensemble est composé de N charges unitaires ( ici sur le dessin N = 7 )

L'énergie de l'ensemble de charges positives sera donc de :
E = N²/2.D0   ( D0 étant la distance moyenne entre les charges positives )

L'énergie de l'ensemble de charges négatives sera aussi de :
E = N²/2.D0   ( D0 étant la distance moyenne entre les charges négatives )

Les deux ensembles ont donc une énergie totale de E = N²/D0

A cela il faut retirer l'énergie d'un ensemble sous l'influence de l'autre, en effet chacun des
deux ensembles est " attiré " par l'autre. Chaque charge unitaire d'un ensemble est attirée
par chaque charge unitaire de l'autre ensemble, ce qui donnera une énergie de E = N²/D1  

On voit donc que quand D1 arrivera à la même valeur que D0  ( la distance moyenne entre les charges
élémentaires a la même valeur pour toutes les charges ) l'énergie totale du système sera nulle.

 

Énergie de deux charges opposées :

      

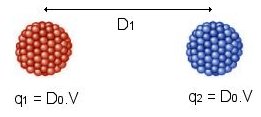
E = (q1)²/2.D0 + (q2)²/2.D0 - (q1).(q2)/D1

Avec q1 = q2, l'énergie totale tend vers zéro quand la valeur de D1 s'approche de la valeur de D0

Avec q1 <> q2, l'énergie totale tend vers (q1 - q2)²/2.D0 quand la valeur de D1 = D0

 

 

Doubler la charge d'une capacité :

      

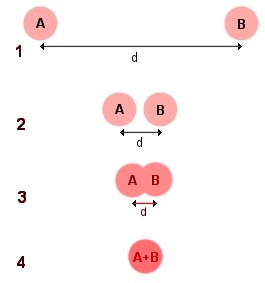
Figure 1
Nous avons deux charges identiques A et B très éloignées l'une de l'autre par une distance d
Ces charges ont une capacité C et un potentiel V, l'énergie de chacune d'elle est de (1/2)C.V²
Soit une énergie totale de C.V²    En fait C, la capacité de chacune d'elle, représente la distance
moyenne entre leurs charges élémentaires.

Figure 2   
Pour diminuer la distance d entre les charges, il faut fournir une énergie de ( q.q' )/d avec
q =q' = C.V = la charge de A et de B. L'énergie totale du système devient
E = C.V² + ( q.q' )/d = C.V² + C².V²/d

Figure 3  
d diminue au point que les charges élémentaires de A et de B se rapprochent et finissent
par former un ensemble de charges éloignées les unes des autres par une distance égale à C.

Figure 4
Ainsi toutes les charges élémentaires du système sont éloignées les unes des autres
par la même distance C et on aura C = d, l'énergie totale du système sera
E = C.V² + ( q.q' )/d = C.V² + C².V²/d = C.V² + ( q.q' )/C = C.V² + C².V²/C = 2C.V²

Pour mettre les deux charges dans une même capacité ( réduire la capacité totale ) Il a donc
fallu ici doubler l'énergie du système.

xxxxxxxxxxxxxx