Conductance ( 1 / Résistance
) ![]()
Conducteur
de charges électriques : ![]()
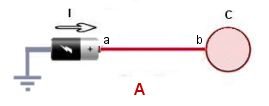
Dans
la figure A ci dessus un pile
électrique charge une capacité C avec une intensité I
Cette intensité est engendrée par une pile, cette pile transmet des charges
à la capacité C
à travers un conducteur ( fil électrique a-b en
rouge sur la figure.)
En
fait ce fil électrique ( en rouge ) transmet des charges, de la pile vers
la capacité C,
qui petit à petit, gagnera du potentiel ( volts ) en supposant
les pertes négligeables. .
L'intensité I = dq / dt transmet chaque seconde des charges vers la droite ( C ) .
Ce
qui transmet des charges électriques ( a-b sur la figure
) se nomme un " conducteur électrique"
ou plus simplement un " conducteur "
Dans
la figure A on pourrait inverser
la pile ce qui changerait le sens de l'intensité.
On voit que une intensité peut avoir deux sens différents positif et négatif.
Conductance
électrique ( Co ) : ![]()
Un
matériaux est dit " conducteur " si, soumis à
une intensité, il laisse passer des charges électriques.
La conductance Co d'un matériaux représente la facilité avec
laquelle il transmet une intensité et donc
des charges électriques. C'est l'inverse de la " résistance
électrique R " ( Co = 1
/ R )
. 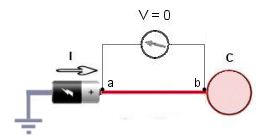
Dans le cas ci dessus on dira que le fil électrique a-b est
parfaitement conducteur si, en lui appliquant
une intensité I, les valeurs de φ
en a et en b ne changent pas, φ(a) -
φ(b ) = constant. ( dφ = 0 )
on dira que la conductance de a-b est infinie, ou bien que
la résistance est nulle.
En
fait comme on ne peut pas mesurer φ directement
en a et en b, la seule manière serait,
au point a et au point b, mesurer le potentiel
et de constater que V(a).= V(b)
Comme on a bien sûr: φ(a) = V(a).dt et φ(b) = V(b).dt donc φ(a)
- φ(b ) = constant.
Une
autre façon d'exprimer que a-b est parfaitement conducteur
ce sera de dire que, soumise
à une intensité I, ( dans un sens ou dans l'autre
), les extrémités a et b n'auront
pas de différence de
potentiel entre elles, V
entre a et b sera toujours nul
Le
travail fourni par une intensité I exercée sur une
distance dφ ( ce travail = I.dφ
) est transformé en énergie,
et comme dφ = 0 aucune énergie sera libérée
dans lle fil a-b : il n'y a pas de pertes d'énergie.
Par contre si au bout d'un certain temps lle fil a-b présente
φ(a) - φ(b ) = dφ >< 0 , la perte d'énergie
sera de I.dφ cette perte d'énergie
apparaîtra probablement sous forme de chaleur.
L'inverse
de la conductance est bien sûr la résistance électrique R
.
Une conductance très grande correspond donc à une résistance
très petite R = 1 / Co.
Un matériaux très " résistant " transmet très
mal une intensité, .Une conductance infinie ( résistance nulle )
correspond à une matériaux " super conducteur" en électricité
classique.
En
général dans une appareil électrique il y a des transferts de
charges d'une partie à l'autre,
mais il faudra bien observer que lorsqu'il y a un transfert d'intensité de
façon continue ce sera
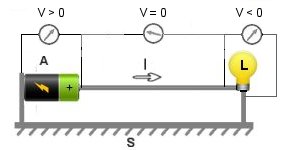
en " circuit fermé ". Dans l'exemple ci dessous, un pile
A dans lequel se trouve une source
d'énergie transmet une intensité dans la lampe L et cette dernière
chauffe, elle acquiert de l'énergie.
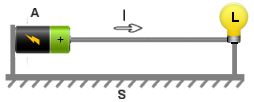
En
fait ce sont des charges qui passent de A vers L,
cette lampe L va acquérir de plus en
plus de charges et gagner de l'énergie. Cette énergie passe
de A vers L, mais pour cela il y a biens
sûr
une base commune S qui met en contact l'ensemble A
et L, sinon la lampe L irait à un potentiel
de plus en plus élevé, jusqu'au potentiel maximum de la pile A
et n'emmagazinerait plus d'énergie.
Dans cette base S il y aura aussi une intensité I
qui sera la même dans tout le circuit.
C'est
pourquoi pour allumer une lampe ou faire tourner un moteur électrique il faudra
au moins deux fils,
avec un seul conducteur on pourra tout au plus charger une capacité, mais
pas transporter de l'énergie
de façon continue..
On
sait que la puissance en électricité se calcule en multipliant l'intensité
par la différence de potentiel.
P = I.V , V étant la différence de potentiel
aux bornes de la pile et I l'intensité du circuit, cette
puissance
représente donc l'énergie libérée par la pile chaque seconde. Cette même énergie
est absorbée par la lampe.
Aux
extrémités de la pile A et de la lampe L
on mesure une différence de potentiel V non nulle, donc
comme il existe une intensité I non nulle, la puissance P
= I.V est positive ou négative suivant
le cas, c'est l'énergie libérée ( par la pile ) et absorbée ( par la lampe
) chaque seconde.
Le
conducteur qui amène les charges à la lampe n'absorbe dans ce cas ci aucune
énergie, il
n'y a pas de différence de potentiel aux extrémités de ce dernier.
L'énergie
libérée par A est donc la puissance multipliée par le temps,
ou encore l'intensité multipliée
par le déplacement φ réalisé.
Comme on ne sait pas mesurer φ directement, on multiplie
la puissance
I.V par le temps écoulé.
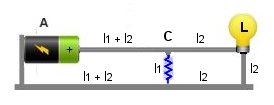
Dans
ce circuit ci dessus on a placé une résistance ( en bleu sur le dessin ) ainsi
une partie de
l'intensité sera déviée et n'arrivera pas à la lampe.
La pile fournit l'intensité totale I1 + I2,
La résistance va prendre une partie de l'intensité ( I1
)
la lampe recevra seulement une intensité I2
En
général la loi de Ohm s'écrit V = I.R ,
comme ici on emploie plutôt la conductance Co = 1/R
on écrira V = I / Co ou encore
I = V . Co
L'intensité
dans un conducteur sera proportionnelle à la différence de potentiel aux extrémités
de ce conducteur et aussi à la conductance de ce dernier. ( si c'est un super
conducteur,
il faudrait une intensité infinie pour maintenir une différence de potentiel
non nulle.)
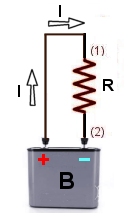
Si
l'on veut maintenir une différence de potentiel entre (1)
et (2), il faudra appliquer
une intensité d'autant plus importante que la conductance de R
est grande. De plus il
faudra
une intensité plus grande si l'on désire augmenter le potentiel V
entre (1) et (2).
Donc on aura bien : I = V . Co
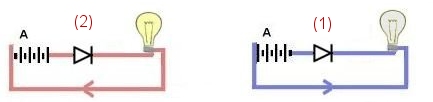
En
électricité il s'agira simplement d'une " diode "
qui laisse passer l'intensité plus facilement
dans un sens que dans l'autre. Si on inverse le sens de la pile de (2)
vers (1) l'intensité dans
le circuit tombe à zéro, car la résistance de la diode
pour un courant inverse est très grande.
Ici la conductance du circuit est différente suivant le sens de l'intensité.
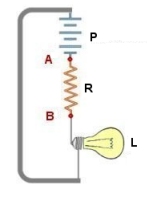
Soit
un " circuit " composé d'une pile qui alimente une lampe
à travers une résistance R .
Aux bornes de cette résistance ( A
) et ( B ) il y aura une différence
de potentiel V = dφ/dt
( équivalente à une différence de rotation dans
le cas mécanique ) avec bien sûr une perte
d'énergie dans la résistance avant d'arriver à la lampe.
Si
maintenant on baisse la température , cette résistance aura
tendance à diminuer, et il se peut que,
brusquement, cette résistance s'annule complètement,
ce qui correspond au cas de " super conducteur ".
Dans ce cas il n'y aura plus de différence de potencieel entre ( A
) et ( B ).
Attention
: En électricité il y a aussi des cas où, en baissant la température la résistance
augmente,
il semblerait que de l'eau ordinaire est plus conductrice que cette même eau
congelée.

La
figure A représente
un conducteur qui transmet une intensité ( I1
) vers la droite,
à la sortie cette intensité sera la même ( I2
).
Les
charges vont donc passer de (1) vers (2)
et seront transmises par ce conducteur.
Si dans ce conducteur, il y a peu de transporteurs de charges ( petites capacités
capables
d'emmagasiner et de transmettre des charges ) ce conducteur est très
" résistant ", les charges
passeront difficilement de (1) vers (2).et
l'intensité transmise ( I2 ) sera la
même mais comme
les charges passent difficilement il faudra une plus grande différence de
potentiel entre (1) et (2)
Par
contre si il y a beaucoup de transporteurs de charges ( figure B
), l'intensité I2 transmise sera
encore la même, mais la différence de potentiel entre (1)
et (2) sera moindre, la résistance aura diminué.
Si la résistance devient nulle, ce dispositif sera " super conducteur
" la différence de potentiel
entre (1) et (2) sera nulle.
Milieu
résistant > < Milieu conducteur : ![]()

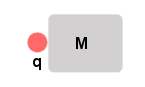
La
figure ci dessus représente une charge q qui rentre en contact
avec un materiau M très résistant .
La charge q conservera toute sa charge et son potentiel,
La charge de q ne va pas se répandre
dans le materiau M, la capacité de la charge q
ne va pas augmenter.
 .
. 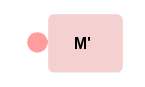

Ici la charge q se rapproche et rentre en contact avec un
matériau conducteur M', la charge q va
se répandre peu à peu dans le milieu M' et, s'ils restent
en contact un certain temps, toute la charge va
rentrer dans le matériau M' pour former une seule charge
avec une capacité plus grande et un potentiel
( voltage ) plus petit.
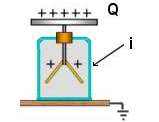
La
figure ci dessus représente une électroscope avec une charge Q
Cette charge sera conservée très longtemps si le matériau i
est un bon isolant électrique,
ce matériau ne laissera pas passer une partie de la charge vers le sol
Isolant
veut tout simplement dire un matériau d'une grande résistance électrique.
On
emploie des isolants électriques pour empêcher des charges de circuler librement
d'un endroit à l'autre.( eviter des "courants de fuites" )