Dimensions Espace Temps

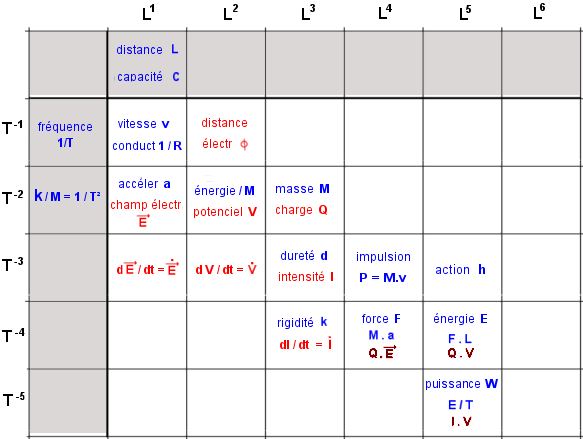
                  v  Représente bien une vitesse ( une longueur divisée par un temps )
                      1/R  Représente la conductance électrique ( inverse de la résistance )

                 a   Représente bien une accélération ( une longueur divisée par un temps au carré )
                           E   Représente le champ électrique 

                 ?  
                         φ Représente le potentiel multiplié par un temps

                v²  Représente le carré d'une vitesse ou le potentiel  ( énergie par unité de masse )
                           V  Représente le potentiel électrique           

                M   Représente la masse
                          Q   Représente la charge 

               d   Représente la dureté ( force divisée par une vitesse )
                      I   Représente l'intensité ( charge par unité de temps ) 

               k   Représente la rigidité ( force divisée par une longueur )
                    ?   Représente la variation d'intensité par rapport au temps

               p   Représente la quantité de mouvement ou impulsion
                    c   Représente un courant ( charge multipliée par une vitesse )            

               F   Représente une force                   

               E   Représente une énergie

               W   Représente une puissance

 

 

Dimensions d'une masse :

 

                            Imaginons nous deux mondes séparés dans lesquels les longueurs sont observées de manières différentes :

                           Dans un monde ( couleur marron ) les longueurs sont le double de celles observées dans l'autre monde ( couleur bleue )
                           

                                  

                           Les vitesses dans le monde marron seront donc le double des vitesses observées dans le monde bleu, il en sera de même
                           pour les accélérations, elles seront observées plus petites dans le monde bleu.                                                            
                            De même dans le monde " bleu " les surfaces seront observées 4 x plus petites et les volumes 8 x plus petits aussi.
                           C'est pourquoi on pourra dire que une surface a comme dimensions L² et les volumes ont comme dimensions L³.

 

----------------------------------------------------

 

                           Imaginons nous maintenant deux mondes séparés dans lesquels les temps ( durées ) sont observés de manières différentes :

                           Dans un monde ( couleur marron ) les espaces de temps sont le double de ceux observés dans le monde bleu
                           Les vitesses dans le monde marron seront donc la moitié des vitesses observées dans le monde bleu, il en sera de même
                           pour les accélérations, elles seront observées quatre fois plus grandes dans le monde bleu

                                    

                              En effet la vitesse V est plus petite que la vitesse V car pour parcourir la même distance on aura mesuré le double du temps                                                                    dans le monde couleur marron. Pour ce qui est de l'accélération on remarque que dans le cas d'un mouvement uniformément
                              accéléré, la distance parcourue d = a.t² / 2, la distance parcourue d étant la même dans les deux mondes il s'en suit que
                              l'accélération a sera quatre fois plus petite que l'accélération a .soit  4.a = a

V                           Voici comment on peut montrer que pour un mouvement uniformément accéléré nous avons d = a.t² / 2 :

                             Soit un point P soumis à une accélération a pendant un temps t

                             Au temps t = 0 la distance parcourue par P est égale à zéro, le point P est encore au repos
                             Après un certain temps t avec une accélération continue a, la vitesse finale sera de a.t. et la vitesse moyenne sera donc de (a.t)/2
                             La distance parcourue sera donc vitesse moyenne x t = d = a.t² / 2   donc si t est mesuré deux fois plus petit avec d constant,
                             il s'en suit que l'accélération a sera mesurée quatre fois plus grande

d = a.t² / 2    =     d = a.t² / 2

d = a.t²    =     d = a.t²

a.t² === a.t²

a x 4.t² === a.t²

a x 4 === a

                             d = d  ( les longueurs sont les mêmes )  et   t = 2 t   On dira que les dimensions de a ( accélération ) est de  L / T²   
                            soit une longueur divisée par un temps au carré   ( l'unité d'accélération sera un mètre par seconde au carré )

                            La vitesse aura pour dimensions une longueur divisée par un temps L/T   ( l'unité de vitesse sera un mètre par seconde )

 

----------------------------------------------------

 

                            Imaginons nous encore une fois deux mondes séparés dans lesquels les longueurs sont observées de manières différentes :                           
                            Dans un monde ( couleur marron ) les longueurs sont le double de celles observées dans l'autre monde ( couleur bleue )

                           Dans chaque monde deux masses m et M séparées par une distance d s'attirent mutuellement suivant la loi d'attraction de Newton
                           avec une force F = (K.M.m)/d² avec K = la constante de Newton. F/m = (K.M)/d² représente l'accélérationa a à laquelle sera
                           soumise la masse m dans chacun des deux cas
                           

                       

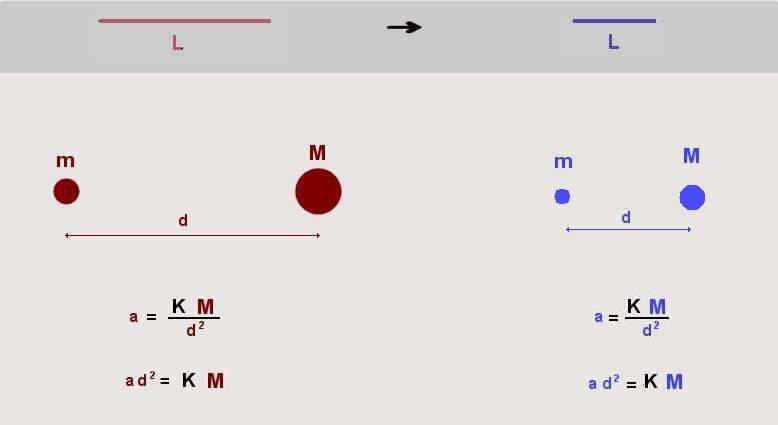
                        Nous avons a = 2 a  et aussi d = 2 d. la valeur de K reste la même dans les deux cas et nous aurons donc M = 8 M
                        Donc on pourra supposer que une masse aura des dimensions en L³   ( avec la même mesure du temps dans les deux mondes )

                       On pourrait aussi remarquer que M a diminué d'un facteur 8 ainsi que son " volume " a diminué d'un même facteur 8, en
                       fait un volume diminue avec la troisième puissance les longueurs. La " dimension " d'un volume sera donc de L³.
                       De la même manière on pourra dire que la " dimension " d'une surface sera de L²

                                           

----------------------------------------------------

 

                          Imaginons nous de nouveau deux mondes séparés dans lesquels les temps sont observés de manières différentes :

                           Dans un monde ( couleur marron ) les espaces de temps sont le double de ceux observés dans le monde" bleu"
                           Les accélérations seront observées quatre fois plus grandes dans le monde "bleu"

                 

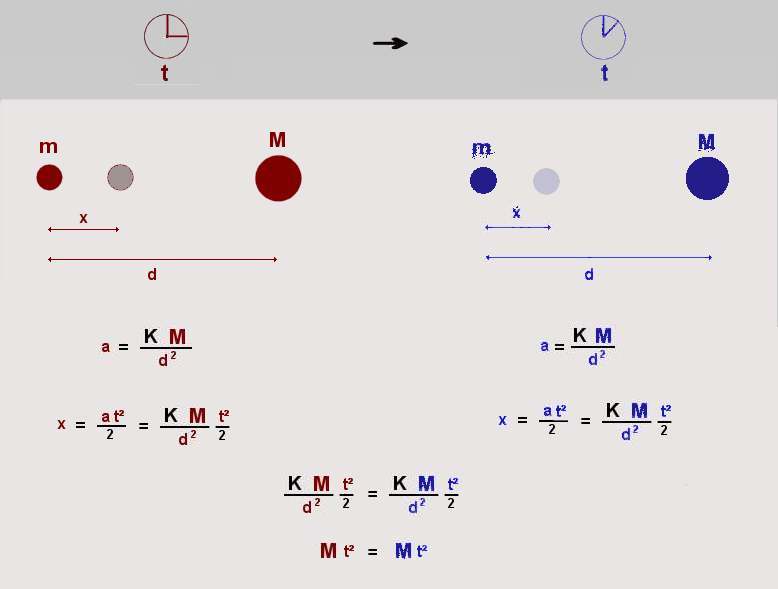
                       Les masses m et m sont attirées par les masses M et M et au bout d'un certain temps t elles se sont déplacées d'une distance x

                       Nous avons donc x = x  et aussi d = d   toutes les longueurs ne changent pas et  t = 2 t  donc dans ce cas   M = 4 M
                       Donc on pourra supposer que une masse aura des dimensions en 1/T²   ( avec les longueurs constantes )

                       On pourrait aussi remarquer que M a augmenté d'un facteur 4, son " volume " n'a pas changé seule sa " masse " a augmenté
                       d'un facteur 4, donc la densité de M a quadruplé.. Les dimensions de la " densité " seront donc 1/T².     

                                     

                        En tenant compte des deux derniers résultats on pourra donc dire que la masse M aura comme dimensions L³/T²

                        On peut le déduire immédiatement : l'accélération de la pesanteur a comme dimensions L/T² ( c'est une accélération )
                        et vaut KM/L² avec K = la constante de Newton, M la masse de la terre et L le rayon de la terre ( une longueur )
                        M/L² est une accéleration L/T² aussi, ils ont donc les mêmes dimensions, on en déduit que M = L³/T²
                        La masse aura donc comme dimensions L³/T² comme ci-dessus

 

                        Une autre manière de se rendre compte de la dimension d'une masse serait de considérer le mouvement d'un pendule simple :

                         T² = L/g   soit    T² = L/ (Mt/R²)   soit encore   T² = LR²/Mt   ( L et R = même dimension L)   ==>  T² = L³/Mt   ==>  Mt = L³/T²

 

 

 

Dimensions d'une charge électrique :

                            

                        En écrivant les formules de l'attraction de deux masses M ( Newton ) et de deux charges Q ( Force de Coulomb )
                        Ce sont deux forces de signse opposés ( attraction et répulsion )             :

 

F   =   (1/R²) MM   =   - (1/R²) QQ    (1)

MM  =   - QQ          (2)

                       Nous avons de chaque côté une " Force " qui doivent donc avoir les mêmes " dimensions "
                       Cette force sera dite " positive " dans le cas d'attraction ( deux masses qui s'attirent suivant Newton ) et " négative ",
                       ( cas de deux charges électriques, positives ou négatives, qui se repoussent suivant la formule de Coulomb )

                       L'équation (2) donne deux solutions pour Q   ==>>   Q = i M   et   Q = - i M   avec   i² = - 1

                      Nous aurons ainsi deux types de charges électriques avec comme dimensions : i M  et  - i M , Ces deux types de charges seront
                     appelées " charge positive " et " charge négative " on verra immédiatement que deux charges de même sens se repoussent
                     ( force négative ) et deux charges de sens contraire auront tendance à se rapprocher ( force positive )

                     De même deux masses positives ou négatives auront tendance à se rapprocher ( force positive ) tandis que deux masses de signes
                     contraires auront tendance à s'écarter l'une de l'autre ( force négative ) suivant la même formules de Newton ( en 1/ R² )

                     Les dimensions de la charge seront donc les mêmes que les dimensions de la masse mais ces dimensions seront complexe,:i L³/T²
                     Beaucoup de grandeurs électriques auront des dimensions " complexe " c'est à dire avec un carré négatif
                     i est un nombre dit " complexe " ou " imaginaire "  défini par la relation :   i² = - 1

                    On pourrait même supposer que une déformation " espace - temps " aurait une partie réelle ( la masse ) et une partie complexe ( la charge )
                    On écrirait donc de façon générale M + iQ et la formule générale d'attracion des" masses - charges"  devient :

F   =   (1/R²) . (M1+iQ1) . (M2+iQ2) . ( 1 - v² / c² ) 

                   On remarque donc que cette force aura deux composantes réelles ( deux masses s'attirent et deux charges de même signe se repoussent )

(1/R²) . (M1.M2)    et    (1/R²) . (iQ1.iQ2)   soit   - (1/R²) . (Q1.Q2)

                   Cette même force aura deux composantes complexes ( une charge n'ayant pas d'effet sur une masse )

(1/R²) . (M1.iQ2)   et   (1/R²) . (M2+iQ1)  

 

                   On remarque que deux charges de même signe vont se repousser et de signe contraire ont tendance à s'attirer   
                 

 

 

                      M.a   =  F         ( 3/-2 + 1/-2 =  4/-4 )     =>  Masse . accélération = Force
                      M.v²  =  E        ( 3/-2 + 2/-2  =  5/-4 )   =>  Masse . carré de la vitesse = Énergie
                      M/R²  =  a       ( 3/-2 - (2/0)  =  1/-2 )   =>  Masse / carré de la distance = accélération   ( g = Mt / R² )
                      M²/R²  =  F      ( 6/-4 - (2/0)  =  4/-4 )   =>  Carré de la masse / Carré de la distance = Force  
                      F.L  =  E          ( 4/-4 + 1/0   =  5/-4 )   =>  Force . distance = Énergie ( travail )
                      F / L  =  k        ( 4/-4 - (1/0)   =  3/4 )   =>   Force / distance = Rigidité ( d'un ressort par exemple )
                      k / M  =  1 / T²    ( 3/-4 - (3/-2)   =  0/2 )   =>   Rigidité / Masse = Carré de la fréquence
                      F . v  =  W      ( 4/-4 + 1/-1   =  5/-5 )   =>   Force . vitesse = Puissance 
                      p / T  =  F     ( 4/-3 + 0/-1   =  4/-4 )   =>   Impulsion / Temps = Force

                      C V  =  Q         ( 1/-0 + 2/-2  =  3/-2 )       =>  Capacité . Potenciel = Charge
                      Q.Ê   =  F         ( 3/-2 + 1/-2  =  4/-4 )      =>  Charge . Champ électrique = Force
                      Q / R²  =  Ê      ( 3/-2 - (2/-0)  =  1/-2 )        =>  Charge / Carré de la distance = Champ électrique
                      Q² / R²  =  F      ( 6/-4 - (2/-0)  =  4/-4 )        =>  Carré de la charge / Carré de la distance = Force
                      V.I   =  W         ( 2/-2 + 3/-3 =  5/-5 )        =>  Potentiel . Intensité = Puissance
                      I / V   =  1 / R      ( 3/-3 - ( 2/-2)  = 1/-1 )     =>  Intensité / Potentiel = Vitesse = Conductance = 1/ Résistance
                      V.V  =  F        ( 2/-2 + 2/-2 =  4/-4 )         =>  Potentiel . Potentiel = Force
                      Q.V  = E        ( 3/2 + 2/-2 =  5/-4 )          =>  Charge . Potentiel = Energie
                      ( I /T ) S   =  V    ( 3/-4 - (1/-2) =   2/-2 )      =>  (Variation d'intensité).( coef self-induct ) = Potentiel

                    (dI/dt.).(coef self-induction) = V   soit    (dI/dt) / V  =  1 / (coef self-induction)  =  L / T²     ==>      T² = (coef self-induction) . L
                    L ici represente une longueur, distance ou capacité     
                   ( La formule classique est T² = LC avec L = coef self-induction et C = capacité )

 

accélération = 1/-2 action = 5/-3 capacité = 1/0 champ électrique 1/-2 champs gravifique 1/-2 charge 3/-2 coef self-induct T²/L = 1/ accélération dureté 3/-3 energie 5/-4 force 4/-4

intensité 3/-3 impulsion 4/-3 masse 3/-2 potentiel électrique 2/-2 potentiel gravifique 2/-2 puissance 5/-5 resistance T/L = 1/ vitesse rigidité 3/-4 vitesse 1/-1